이분 탐색,이진 탐색(Binary Search) 알고리즘에 대해 알아보자. ( Java )
백준문제를 풀다가 이분 탐색을 사용하게 된 문제가 있어서 글을 써본다.
먼저 이분탐색이란 주어진 정렬된 리스트에서 특정한 값을 찾는 알고리즘으로, 리스트를 반으로 나누어 탐색 범위를 좁혀가며 원하는 값을 찾아가는 방식이다.
이 알고리즘은 매우 효율적으로 동작하고, 탐색 대상이 많은 큰 데이터 집합에서 유용하게 사용된다. 이분탐색은 O(log N)의 시간 복잡도를 가진다.
이분탐색 알고리즘을 글로 설명하자면 다음과 같다.
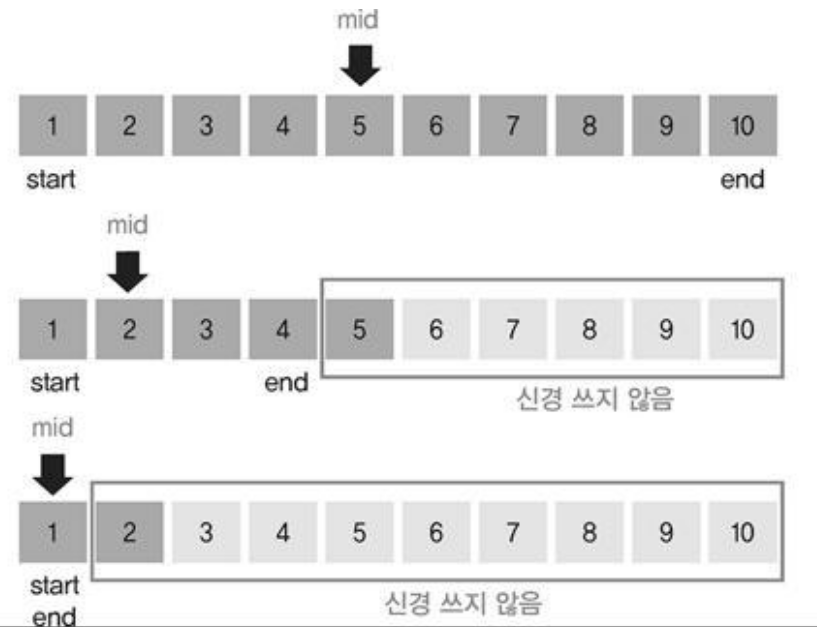
1. 처음에 주어진 리스트의 초기 인덱스와 끝 인덱스를 받아 2로 나누어 가운데 값을 구한다.
ex) mid = (low + high ) / 2
2. 주어진 리스트는 정렬되어 있으므로 리스트의 mid에 위치하는 요소와 찾고자 하는 요소를 비교한다.
이때, 찾고자 하는 요소인 key 값이 mid의 요소와 같다면 값을 찾은 것이므로 종료하고
mid의 요소값이 찾고자하는 key 값보다 작다면 key값은 현재 mid 보다 큰 쪽에 있으므로 다시 큰 쪽 절반에 대해서 이분탐색을 수행한다.
반대로, mid의 요소값이 찾고자 하는 key 값보다 크다면 key값은 현재 mid보다 작은 쪽에 있으므로 다시 작은 쪽 절반에 대해서 이분탐색을 실행한다.
3. 이렇게 반복을 해서 mid의 요소값과 key 값이 같을 때 까지하고 찾고자 하는 요소값이 리스트에 존재하지 않고, 탐색범위가 더 이상 없다면 주어진 리스트에 찾고자 하는 값이 없으므로 종료가 된다.
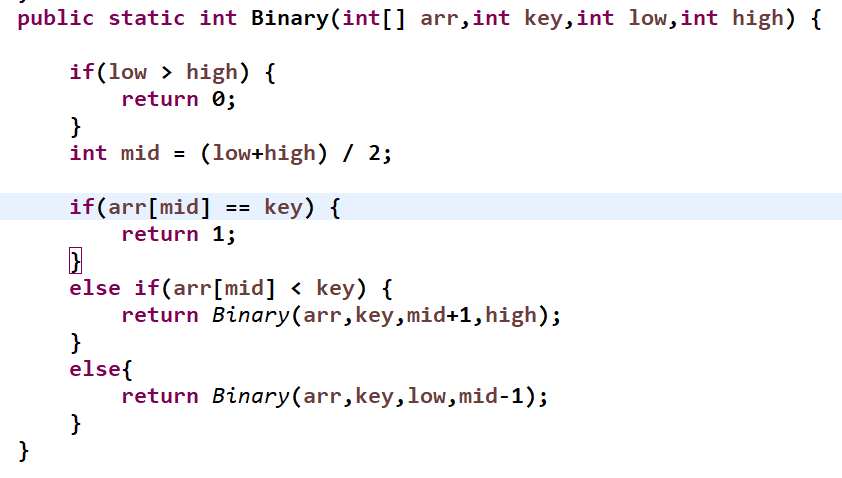
자바코드를 통한 이분탐색 예시이다.
코드를 보면 arr[mid]를 기준으로 key값과 비교를 통해 범위를 좁혀나가고 있다.
if(low > high) {
return 0;
}
이 코드를 통해서 low 와 high의 위치가 역전되었을 경우 찾고자 하는 요소값이 없다는 것을 의미하므로 0을 반환한 모습이다.